• Waarderen bij echtscheiding

    Het waarderen van een onderneming bij echtscheiding is bijzonder omdat het doorgaans gedomineerd wordt door emoties. Als partijen lijnrecht tegenover elkaar komen te staan wordt er een deskundige aangesteld om uiteindelijk de waarde van de onderneming vast te stellen. De deskundige wordt in zijn opdracht geconfronteerd met spraakverwarring en emoties die zijn werk soms bemoeilijken. De spraakverwarring is meestal terug te brengen tot onjuiste kennis en toepassing van de waarderingstechnieken en niet consistente of onjuiste uitgangspunten hanteren in de waardering. De emoties hebben soms op beide aspecten invloed om een doelredenering te ondersteunen.

door: Chris Denneboom

In een echtscheidingsprocedure lopen emoties soms hoog op. Wanneer er een onderneming in het spel is dan is de waardering van de onderneming of de aandelen een belangrijk aandachtspunt. De waarde van een onderneming wordt bepaald door de toekomstige verwachte rendementen. Deze verwachtingen zijn subjectief. Als partijen lijnrecht tegenover elkaar staan dan gebeurt het regelmatig dat de subjectieve verwachtingen inzake de onderneming sterk beïnvloed worden door doelargumenten om tot een bepaalde waarde te komen. Wanneer de rechter geen oordeel kan vellen op basis van de door partijen aangevoerde argumenten wordt vaak een beroep gedaan op een waarderingsdeskundige.

Deze deskundige krijgt één of meer door partijen geformuleerde vragen die beantwoord dienen te worden. Omdat de rechter lijdelijk is in het civiel recht wordt de omvang van het geschil bepaald door de partijen zelf. Binnen de omvang van het geschil en de geformuleerde vragen is het soms manoeuvreren om vaktechnisch juiste antwoorden te geven op de vragen binnen de begrenzingen van het kader van de opdracht. Verschillen in juridische betekenis, het algemeen spraakgebruik en economische betekenis tussen begrippen zijn vaak de oorzaak dat opdrachten voor waarderingsdeskundigen onduidelijk geformuleerd lijken of de waardeerder in zijn uitoefening van zijn vak beperkt.

Thema’s

Bedrijfswaardering (12) Belasting Magazine (5) Familieoverdracht (6) Financieel Management (11) PE Tijdschrift voor Bedrijfsopvolging (8)

De waarderingsmethode

Wanneer mensen die zich regelmatig met bedrijfswaardering bezighouden het hebben over waarde bedoelen ze bijna altijd economische waarde. Deze wordt berekend door toekomstige rendementen of geldstromen te disconteren ofwel een vorm van discounted cash flow berekening toe te passen. Wanneer buitenstaanders van het vak het hebben over waarde dan is er een haal scala aan termen die de waarde uitdrukken. Begripsverwarring ligt op de loer en met een sausje emotie en doelredenering wordt de discussie ineens heel complex. Ik zal de meest gebruikte termen nader uitleggen.

Rentabiliteitswaarde

Veelal wordt er gemakshalve bij een waardering bij echtscheiding uitgegaan van het winstbegrip en de rentabiliteitswaarde methode. Dit is een eenvoudig methode die ook te volgen is door niet specialisten en je kan de inputvariabelen aflezen uit de jaarrekening. Het winstbegrip is in principe een foute grondslag, immers winst is vooral fiscaal gedreven. Het wordt beïnvloed door afschrijvingen die geen uitgaven zijn. De hoogte van de afschrijvingen is daarnaast doorgaans een fiscale keuze en kan bovendien van jaar tot jaar wisselen. Daarnaast kunnen voorzieningen op de balans zorgen dat de winst beïnvloedt wordt zonder dat er echt geld stroomt. Meestal worden deze effecten in een waardering op basis van rentabiliteitswaarde gecorrigeerd door normalisaties in de winst toe te passen.
Het volgende bezwaar van de rentabiliteitswaarde berekening is dat er maar één geldstroom beschouwd wordt voor de waardering. In de procedure wordt dit soms als een voordeel gezien omdat de discussie van een prognose vermeden kan worden. Vaak wordt dan een historisch genormaliseerd gemiddelde gehanteerd. Reële groei of krimp van de onderneming wordt, door deze methode te hanteren, niet in ogenschouw genomen. Anders gezegd men veronderstelt dat de onderneming een stabiel rendement maakt waarbij investeringen en afschrijvingen gelijk zijn en dat er geen mutatie in werkkapitaal is. Dit zal zeker niet altijd het geval zijn maar soms ook wel. Wanneer dit het geval is dan begint de berekening erg te lijken op de restwaarde berekening van een discounted cash flow waardering.

Download dit artikel in PDF-formaat

DOWNLOAD

Disconteringsvoet

De disconteringsvoet is het percentage waartegen toekomstige geldstromen contant worden gemaakt. In dit percentage zit de tijdvoorkeur voor geld en het aanwezige risico verwerkt. Bij de rentabiliteitswaarde wordt de waarde van het eigen vermogen uitgerekend. De rendementseis in de berekening dient dan ook de rendementseis op het eigen vermogen te zijn en niet de gemiddelde kostenvoet van het totaal vermogen, ook wel eens de WACC genoemd. Om meer specifiek te zijn het dient de rendementseis op het eigen vermogen levered te zijn. Anders gezegd rekening houdend met de inbreng van vreemd vermogen. De kostenvoet eigen vermogen levered laat zich via de volgende formule uitrekenen


Kel = Keu + (Keu -/- Kv) x VV/EV
Kel = kostenvoet eigen vermogen levered
Keu = kostenvoet eigen vermogen unlevered (zonder inbreng van vreemd vermogen)
VV = vreemd vermogen
EV = eigen vermogen.
De berekende Kel geeft uitdrukking aan het rendement op het eigen vermogen door de inbreng van vreemd vermogen. Volgens de gangbare waarderingstheorie is de wijze van financiering niet van invloed op de waarde van een onderneming. Slechts het belastingvoordeel op de renteaftrek van vreemd vermogen zorgt voor een (beperkte) waarde toename in de vorm van een tax shield. In formulevorm is dat:


Vl=Vu + Tc x D
Vl = value levered, ondernemingswaarde met inbreng van vreemd vermogen
Vu = value unlevered, ondernemingswaarde zonder de inbreng van vreemd vermogen
Tc = tax, belastingtarief
D = debt, waarde van het vreemd vermogen
Wanneer vervolgens de winst na belasting gedeeld wordt door de Kel dan krijg je de waarde van het eigen vermogen. Deze berekening is alléén juist als de eerdere aannames van toepassing zijn, namelijk: dat de onderneming in een stabiele situatie verkeert en er dus geen reële groei of krimp aanwezig is, dat de investeringen en de afschrijvingen gelijk zijn en er geen mutatie werkkapitaal is. Tevens dient ook nog te gelden dat de verhouding eigen vermogen / vreemd vermogen niet meer wijzigt. Als dit van toepassing is dan is de rentabiliteitswaarde gelijk aan een cash to equity berekening wat weer een vorm van DCF waardering is.
Met bovenstaande berekening zijn we er echter nog niet. Ik gaf aan dat er geen reële groei aanwezig is maar er is bijna altijd wel sprake van nominale groei ofwel het in pas blijven lopen met de economische groei of inflatie. Om dit tot uiting te laten komen dient inflatie aan de berekening te worden toegevoegd. In plaats van de winst gaan we uit van de verwachte winst na één jaar ofwel winst vermeerderd met de inflatie.


W1 = W0 x (1+inflatie)
En in plaats van te delen door de Kel delen we door de Kel -/- de inflatie. De formule om de waarde van het eigen vermogen uit te rekenen wordt dan als volgt:

W1
Vev = (Kel – infl)
Voor de berekening van de Kel is de verhouding eigen vermogen en vreemd vermogen nodig. Bij deze verhouding wordt niet de boekhoudkundige waarde bedoeld maar de berekende economische waarde van het eigen vermogen in de bovenstaande formule in relatie tot het aanwezige vreemd vermogen.
Doorgaans wordt de boekhoudkundige waarde van het vreemd vermogen gelijk gesteld aan de economische waarde van het vreemd vermogen. Dit is echter alleen het geval wanneer de geldende contractrente van het vreemd vermogen gelijk is aan de marktrente. Is dit niet zo dan wijkt de economische waarde van het vreemd vermogen af. Wanneer de contractrente hoger is dan de marktrente dan is de economische waarde van het vreemd vermogen hoger dan de boekhoudkundige waarde en wanneer de contract rente lager is dan is de economische waarde van de schulden lager dan boekhoudkundige waarde. Het verschil kan uitgerekend worden door de rente en aflossing contant te maken tegen de marktrente. Een hogere economische waarde van het vreemd vermogen betekent een lagere economische waarde van het eigen vermogen.

Verbeterde rentabiliteitswaarde

Vaak wordt er onder het mom van de verbeterde rentabiliteitswaarde nog een correctie uitgevoerd voor oversolvabiliteit. Daarmee wordt bedoeld dat de boekhoudkundige waarde van het eigen vermogen hoger is dan doorgaans in de branche gebruikelijk is. Het verschil zou uitgekeerd kunnen worden en bij de waarde opgeteld moeten worden. Hier dreigt het gevaar dat boekhoudkundige principes en economische principes door elkaar heen gaan lopen. We berekenen de economische waarde van het eigen vermogen. Het verschil tussen de economische waarde van het eigen vermogen en de boekhoudkundige waarde van het eigen vermogen is de boekhoudkundige goodwill. In de waardering is al rekening gehouden met de verhouding vreemd en eigen vermogen in de Kel berekening. Deze correctie die veelvuldig gedaan wordt is dus niet terecht en onjuist. Wat echter wel het geval kan zijn is dat er liquide middelen of andere niet operationele activa op de balans kunnen staan. Niet operationele activa zijn activa die niet dienstbaar zijn aan de exploitatie en onttrokken kunnen worden aan de balans zonder dat het invloed heeft op de exploitatie. De waarde van de niet operationele activa wordt wel bij de berekende waarde van het eigen vermogen opgeteld. Ik zal het geheel duidelijk maken aan de hand van een rekenvoorbeeld.

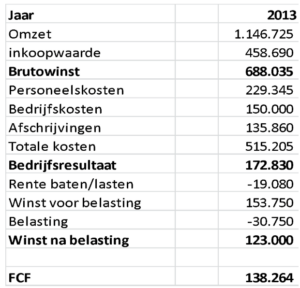
Als we de waarde uitrekenen volgens de rentabiliteitswaarde methode dan gaan we uit van het resultaat na belasting op W1. Dat is het resultaat in 2013 vermeerderd met inflatie. Echter de rentelasten dienen niet voor inflatie gecorrigeerd te worden. Bij waarderen gaan we uit van de jaarconventie. Dat wil zeggen dat verondersteld wordt dat alle geldstromen één keer per jaar stromen en wel per einde boekjaar. Voor het vreemd vermogen betekent dat dus dat de rente berekend wordt over de stand van het vorige boekjaar omdat eventuele aflossing pas plaats vindt per einde boekjaar. In het cijfervoorbeeld was er geen aflossing in 2013 vandaar dat de rentelast in 2013 en 2014 (W1) gelijk zullen zijn. We krijgen dan bij een inflatie van 2% de volgende rekensom:


172.830 *(1+2%) = 176.287 bedrijfsresultaat
– 19.080 rente
= 157.207 resultaat voor belasting
– 31.441 belasting
= 125.765,28 resultaat na belasting
De inflatie over het vreemd vermogen dient echter ook nog in de berekening meegenomen te worden omdat we veronderstellen dat vermogensverhouding gelijk blijft. We tellen daarom bij het resultaat na belasting nog op de inflatie op het vreemd vermogen (2% x 318.000= 6.360).


125.765 + 6.360 = 132.125,28 = W1

In onze berekening gaan we uit van
Keu = 16%
Kv = 6%
Belasting = 20%
Inflatie = 2%

De rentabiliteitswaarde is:

W1
Vev = (Kel – infl)
Kel = Keu+(Keu – Kv) x VV/Vev
We zien dat de onderste formule afhankelijk is van de uitkomst van de bovenste formule. Als we dit in Excel als formules bouwen en we zetten iteratie aan dan is de uitkomst van Kel = 20,43757% en als we W1 delen door Kel minus inflatie dan krijgen we:

132.125,28
Vev = 20,43757%-2% = 716.609

Als we uitgaan van een discounted cash flow waardering volgens de APV methode dan maken we de vrije geldstroom (FCF) op t=1 contant tegen Keu minus inflatie en vervolgens maken we de renteaftrek op het vreemd vermogen contant tegen Keu minus inflatie. Dit levert samen de ondernemingswaarde op.

138.264 x 1.02 / (16%-2%) = 1.007.352
19.080 x 20% / (16%-2%) = 27.257
Ondernemingswaarde = 1.034.609

Als we daar vervolgens de waarde van het vreemd vermogen van aftrekken dan krijgen we de waarde van het eigen vermogen.


1.034.609 – 318.000 = 716.609
Bovenstaande toont aan dat de berekening gelijk is aan de eerdere rentabiliteitswaarde berekening.

Rekenkundig geven beide methodes dezelfde uitkomst. Echter om hiertoe te komen hebben we een aantal uitgangspunten gehanteerd waarvan het de vraag is of zij juist zijn. We hebben de investeringen aan de afschrijvingen gelijk verondersteld en de werkkapitaalmutatie op nul, waardoor het bedrijfsresultaat na belasting gelijk is aan de vrije geldstroom. Als we echter naar de balans kijken dan zien we het netto werkkapitaal in 2013 toenemen van 143.137 naar 146.000. De berekende vrije geldstroom is dus 2.863 te hoog. Onze veronderstelling van geen werkkapitaalmutatie klopt dus niet. Ook wanneer een onderneming zich in een stabiele fase bevindt dan groeit het werkkapitaal mee met de inflatie. Een juiste DCF waardering zou dus een lagere uitkomst hebben gehad als we de werkkapitaalmutatie wel meegenomen zouden hebben. Het verschil bedraagt:


(2.863 x 1.02) / (16%-2%) = 20.857

Daarnaast is de vraag gerechtvaardigd of het vreemd vermogen in een vaste verhouding meegroeit met de waarde van de onderneming. Logisch zou zijn dat het vreemd vermogen stabiel blijft op een bepaald bedrag of zelfs daalt naar de toekomst door aflossingen. Door de aflossingen buiten beschouwing te laten wordt de waarde van de tax shield overschat.

Als we naar het onderdeel verbeterde rentabiliteitswaardemethode kijken dan zien we dat in boekhoudkundige termen de solvabiliteit 50% bedraagt. Wanneer de boekhoudkundige streefwaarde van 30% als norm gehanteerd zou worden dan betekent het dat we 237.000 winst zouden kunnen uitkeren. Het eigen vermogen zou dan 188.000 bedragen op een balanstotaal van 621.000. De verbeterde rentabiliteitswaarde zou dan uitkomen op 953.609.

Kijken we echter naar de economische waarde dan is alleen maar de vraag van belang hoeveel van de aanwezige liquide middelen is dienstbaar aan de onderneming en hoeveel zou er onttrokken kunnen worden aan de onderneming zonder dat de exploitatie van de onderneming daar hinder van ondervindt? Als we zouden uitgaan van het feit dat de liquide middelen volledig onttrokken zouden kunnen worden en derhalve niet operatoneel zijn dan zou de economische waarde van het eigen vermogen met 300.000 toenemen. Hierdoor zou de economische waarde van het eigen vermogen uitkomen op 1.016.609 hetgeen hoger is dan de berekende verbeterde rentabiliteitswaarde. De liquide middelen zouden ook aangewend kunnen worden om het vreemd vermogen met 300.000 af te lossen. De uitkomst zou in dat geval hetzelfde zijn met dat verschil dat het toekomstige vreemd vermogen 300.000 lager is en dus ook de tax shield berekend moet worden over dit lagere bedrag. De uitkomst zou in dit geval 990.895 bedragen.

Bovenstaande balans toont dezelfde balans als eerder maar dan zijn voor de waardering de liquide middelen aangewend voor het aflossen van de schuld. Als we dan de verbeterde rentabiliteitsmethode toepassen:


172.830 *1.02 = 176.287 bedrijfsresultaat
– 1.080 rente
= 175.207 resultaat voor belasting
– 35.041 belasting
= 140.165,28 resultaat na belasting

140.165,28 + (2% x 18.000)
Ve = (16,18165% – 2%) = 990.895

De winst wordt aangepast met een lagere toekomstige rentelast. Daarnaast berekenen we de inflatie over de lagere schuld. De Kel daalt omdat de hoeveelheid vreemd vermogen minder wordt. Volgens de traditionele verbeterde rentabiliteitswaarde methode zou nog een forse oversolvabiliteit bestaan. Omdat er nu geen liquide middelen meer zijn krijgen we geen balansverkorting meer. Afromen van de solvabiliteit zal gaan in de vorm van substitutie van eigen vermogen voor vreemd vermogen. De norm was 30%. Dat betekent dat het eigen vermogen 30% van 558.000 moet bedragen wat neerkomt op een bedrag van 167.400 en een correctie op de waarde van 257.600 waardoor de totale waarde van het eigen vermogen op 1.248.495 uit zou komen. Deze uitkomst is absoluut verkeerd.

De juiste methode is om de balanswaarden te verwerken met de veronderstelde vermogensverhouding en de berekening opnieuw te maken. We krijgen dan als uitkomst een waarde Ve van 755.375 als we dit vermeerderen met de uitgekeerde solvabiliteit van 257.600 komen we op een totaal van 1.012.775 wat gelijk is aan de berekende waarde volgens de APV bij deze financieringsstructuur. Dit voorbeeld illustreert ook hoe belangrijk het is om voor de rentabiliteitswaarde berekening uit te gaan van de Kel en de daarbij behorende vermogensverhouding. Niet zelden zie ik dat er een vermogenskostenvoet of disconteringsvoet bepaald wordt die niet aangepast wordt aan de leverage hetgeen tot onjuiste uitkomsten leidt en tot grote afwijkingen met de economische waarde.

Moraal van het verhaal is dat de rentabiliteitswaarde methode een hoop paralellen heeft met discounted cash flow methodes. Worden de uitgangspunten en de systematiek consistent en juist gevolgd dan geeft deze eenzelfde uitkomst als bij een DCF waardering. Echter door subtiele interpretatiefouten van de methodiek of de uitgangspunten kan de uitkomst volledig van de werkelijkheid gaan afwijken.

Intrinsieke waarde

De intrinsieke waarde van de aandelen is de zichtbare waarde van eigen vermogen op de balans. De jaarrekening wordt opgesteld op boekhoudkundige principes dus de intrinsieke waarde geeft geen beeld van de economische waarde. Vaak wordt bij een waardering van aandelen in het kader van echtscheiding gevraagd naar de intrinsieke waarde van de aandelen en de aanwezige goodwill. Als we uitgaan van de economische waarde van een onderneming als enige juiste maatstaf dan dient bovenstaande vertaald te worden. Het verschil tussen de economische waarde van een onderneming en de boekhoudkundige waarde is weergegeven in onderstaande schematische balans.

Economische balans
Stille reserves Economische   Economische waarde EV
Goodwill waarde Economische waarde VV
Boekwaarde activa
Werkkapitaal Boekwaarde
Niet operationele activa
Ondernemingswaarde Ondernemingswaarde

De boekhoudkundige waarde van de activa, het werkkapitaal en de niet operationele activa vormen samen de boekhoudkundige ondernemingswaarde ofwel het balanstotaal. Gaan we naar de economische waarde dan verschilt dat met de hoogte van eventuele aanwezige stille reserves en goodwill. De ondernemingswaarde is onder te verdelen in eigen vermogen en vreemd vermogen. Bij de economische waarde gaan we er van uit dat alleen rentedragende schulden tot het vreemd vermogen behoren. Overige kortlopende schulden worden beschouwd als werkkapitaal. De boekhoudkundige waarde van de schulden kan afwijken van de economische waarde zoals eerder besproken. Dit leidt in economische zin tot een directe aanpassing in de economische waarde van het eigen vermogen. Dit principe dient goed in ogenschouw genomen te worden als men beoogt met de intrinsieke waarde de economische waarde van het eigen vermogen weer te geven. We zullen het een en ander weer duidelijk maken met een cijfervoorbeeld.

Bovenstaande balans is de balans van de holding van de heer Aalbers. Ten behoeve van zijn echtscheiding dienen de aandelen gewaardeerd te worden. Gevraagd wordt de intrinsieke waarde van de aandelen vermeerderd met eventueel aanwezige stille reserves en goodwill. In de holding vindt geen andere activiteit plaats dan het verlonen van de heer Aalbers. De exploitatie toont het volgende beeld:

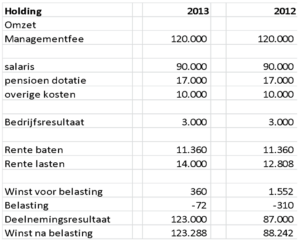
Bij de waardering van de aandelen van de holding is een DCF waardering mogelijk maar we dienen ons wel te realiseren dat binnen de holding diverse activiteiten aanwezig zijn die allen een eigen risicoprofiel kennen en dus ook een dienovereenkomstige rendementseis vergen. Het is daarom praktisch om de economische waarde van de onderdelen apart te bepalen rekening houdend met het eigen risicoprofiel. Bij echtscheidingen maar ook bij andere geschillen komt het bovendien nog wel eens voor dat partijen per onderdeel uitgangspunten ter discussie stellen. Dit is nog een reden om de onderdelen individueel te waarderen. Hierbij dient het vennootschappelijk resultaat van de holding en de diverse onderdelen op de balans gewaardeerd te worden. We laten het vennootschappelijk resultaat voor alsnog buiten beschouwing. Hieronder lopen we de balans stap voor stap door.

  • ValuePro case bedrijfswaardering: geschil met aandeelhouders
  • ValuePro case partijdeskundige bij faillissement
  • drs. Chris Denneboom RV RAB professional in bedrijfswaardering en gerechtelijk deskundige

De uitgangspunten

Waardering deelneming

Als eerste zien we de deelneming. Dat is de deelneming die we eerder gewaardeerd hebben op afgerond 1 mlio. De vraag is of het klopt dat het resultaat en de cashflow van de deelneming over 2013 representatief zijn voor de toekomst. Als dit niet zo is dan kan er per definitie niet meer met de rentabiliteitswaarde gewerkt worden maar dient er een twee fasen waardering volgens het discounted cash flow principe gemaakt te worden. Een scenarioperiode en een restwaardeperiode. In dit geval gaat het erom hoe tot een redelijke prognose gekomen kan worden wanneer partijen van mening verschillen. Kijken we naar het deelnemingsresultaat 2012 dan zien we dat dit 1/3 lager is dan 2013. Dit is al een indicatie dat de stabiele situatie mogelijk niet aan de orde is. De heer Aalbers heeft als belang dat de aandelen zo laag mogelijk gewaardeerd worden en zijn ex vrouw heeft een tegenovergesteld belang. De heer Aalbers bepleit dan ook dat het resultaat 2013 incidenteel hoog was. Zijn ex vrouw geeft aan dat dit resultaat verre van incidenteel was en dat de groei nog verder door zal zetten. Om tot een juiste waardering te komen dient de waardeerder dus een reële prognose te maken. Om dit te doen zal hij zich moeten verdiepen in de onderneming en in de markt waarin de onderneming opereert. Daarnaast zal hij zowel de heer Aalbers als zijn ex vrouw horen over hun argumenten voor hun respectievelijke toekomstverwachtingen. Op basis van deze informatie dient de waardeerder een prognose op te stellen die in lijn ligt met de marktontwikkelingen, de concurrentiepositie en de capaciteiten van de onderneming. Ook dient er een consistente prognosebalans opgesteld te worden waarin de benodigde investeringen en werkkapitaalmutaties zijn verwerkt. Wij gaan er in ons verdere voorbeeld vanuit dat partijen het eens zijn dat 2013 representatief is voor de toekomstige resultaten.

Waardering lening u/g

De ex vrouw van de heer Aalbers bepleit dat de lening aan privé onzakelijk is omdat een te lage rente wordt gerekend. Hierdoor zijn de rentelasten te laag en zijn de aandelen te laag gewaardeerd.
De lening dient bezien te worden als een belegging, vergelijk het met een obligatie. Als een obligatie op de beurs genoteerd staat en de rente stijgt dan daalt de waarde van de obligatie en omgekeerd. Om vast te stellen of de lening al dan niet zakelijk is dient de overeengekomen rente vergeleken te worden met de geldende marktrente op het moment dat de overeenkomst gesloten werd. Als de marktrente voor leningen met een vergelijkbaar risico op het moment van de overeenkomst inderdaad hoger was dan is de lening inderdaad onzakelijk in economische zin. In dit geval kan worden uitgegaan van de boekwaarde van de lening. Immers de boekwaarde en de economische waarde zijn aan elkaar gelijk als het rendement op de lening gelijk is aan de marktrente. Door uit te gaan van de boekwaarde repareren we dus de vermeende onzakelijkheid. Als de rente op het moment van de overeenkomst wel zakelijk is vastgesteld maar de huidige marktrente is hoger betekent het dat de waarde van de lening lager is dan de boekwaarde. Het verschil laat zich uitrekenen door de contante waarden van de rente en aflossingen uit te rekenen. Het verschil dient gecorrigeerd te worden op de intrinsieke waarde van de aandelen.

Waardering effecten

De effecten op de balans staan conform de grondslagen in de jaarrekening tegen de historische verkrijgingsprijs. De werkelijke waarde van de effecten is conform de opgave van de bank per balansdatum 100.000 hoger dan de verkrijgingsprijs. De intrinsieke waarde dient aangepast te worden met het verschil tussen de boekwaarde en de werkelijke waarde minus het belastingeffect over de winst of het verlies.

Rekening courant DGA en liquide middelen

De rekening courant met de DGA en de liquide middelen zijn de boekwaarde en de economische waarde gelijk waarbij we veronderstellen dat beide dagelijks opeisbaar zijn en dat de rente gelijk is aan de marktrente. Daarnaast gaan we er van uit dat de liquide middelen in de holding onttrokken kunnen worden zonder dat de bedrijfsvoering daar hinder van ondervindt.

Waardering Pensioenvoorziening

Aan de passief zijde van de balans zien we de pensioenvoorziening. Een pensioenvoorziening is vreemd vermogen. Net zoals bij alle vreemd vermogen dienen we uit te gaan van de economische waarde van het vreemd vermogen. De pensioenvoorziening staat tegen de fiscale waarde op de balans. Herrekening naar economische waarde of in pensioentermen, commerciële waarde, kan het beste gedaan worden door een pensioenspecialist. Het verschil in boekwaarde en economische waarde wordt vervolgens weer, rekening houdend met het belastingeffect, gecorrigeerd op het eigen vermogen. Voor ons voorbeeld gaan we uit van een commerciële waarde van het pensioen van 550.000 per balansdatum.

Resumerend zouden de waarde van de aandelen van de holding als volgt berekend worden:

Waarde economisch verkeer of economische waarde?

Deze begrippen worden nogal eens met elkaar verward. Wij zijn tot nu toe uitgegaan van de economische waarde. Dat lijkt het meest logische omdat we bij een echtscheiding de subjectieve waarde willen weten van de geldstromen die een partij gaat missen door de scheiding. De waarde economisch verkeer is iets anders. Dat is het bedrag dat een zaak zou opbrengen als deze zou zijn verkocht op de vrije markt. We hebben het hier dus over de prijs die door onderhandeling tot stand zou zijn gekomen. Waarde en prijs zijn twee verschillende begrippen en kunnen flink van elkaar verschillen. Soms wordt bij echtscheidingen in de discussie betrokken wat de prijs zou moeten zijn voor 50%. Vaak is bij een MKB onderneming 50% nagenoeg onverkoopbaar en dus ook nagenoeg waardeloos. Soms kan de prijs ook hoger zijn dan de stand alone waarde als synergetische waarde wordt toegevoegd door een strategische koper. Als er al uitgegaan zou moeten worden van een prijs dan zou het de prijs moeten zijn voor 100% van de aandelen die vervolgens pro rato toegekend wordt aan het belang in de boedel van de ex echtgenote. De gedachte hierachter is dat de prijs op het totaal binnen de gemeenschappelijke boedel valt en deze verdeeld dient te worden. Wanneer de echtelieden ieder 50% van de aandelen zouden hebben en er is geen gemeenschap dan is het een ander verhaal. De prijs is dan het beste bod in de vrije markt. De vraag is of dit redelijk en billijk is. Deze afweging is echter niet aan de waarderingsdeskundige maar aan de rechter. Afstemmen vooraf over wat de grondslag voor de waardering is, is dus noodzakelijk om niet verstrikt te raken in een opdracht waarvan het consistente antwoord niet het antwoord is dat partijen bedoelen.

Waarde en alimentatie

Een DGA heeft de vrijheid om de hoogte van het inkomen, binnen bepaalde kaders, zelf te bepalen. De hoogte van dit inkomen is van invloed op het rendement van de onderneming. In ons voorbeeld is dit een samenstelling van doorberekende management fee aan de werkmaatschappij en het loon in de holding. Om tot een juiste waardering te komen dient de management fee op het niveau gesteld te worden zodat het overeenstemt met een gebruikelijke fee voor de aard en omvang van de onderneming afgezet tegen objectieve marktgegevens. Hierbij dient in ogenschouw genomen te worden een normale arbeidsbeloning voor de DGA in de holding, in overeenstemming wat in de markt gebruikelijk is vermeerderd met de kosten die via de holding verlopen. Wanneer het vennootschappelijke rendement positief of negatief is dient bezien te worden waar dit positieve of negatieve rendement aan toe te schrijven is. In ons voorbeeld is er een klein positief bedrijfsresultaat van 3.000. Omdat de operationele activiteiten in de deelneming zijn ondergebracht dienen we door de balans heen te kijken en dit resultaat eigenlijk toe te schrijven aan de deelneming en tegen de rendementseis van de deelneming contant te maken. Een alternatief kan zijn om de managementfee fictief aan te passen zodat het bedrijfsresultaat op nul loopt in de holding. Wanneer de DGA echter een wezenlijk deel van zijn tijd besteed aan het beheren van de beleggingen in de holding dan zou de management fee vanuit de werkmaatschappij alleen toereikend moeten zijn voor het deel van de tijd dat de DGA aan de werkmaatschappij besteed. Het resterende deel zou gedekt moeten worden uit de rendementen van de beheerde beleggingen.

De aanpassingen van het inkomen voor de waardebepaling zijn eveneens van invloed op de draagkrachtberekening voor de alimentatie. Een hoger inkomen leidt tot een lager rendement en dus een lagere ondernemingswaarde en vice versa. Vaak wordt de hoogte van het inkomen ten behoeve van een alimentatieberekening apart behandeld van de waarde van de aandelen. De waardeerder dient hier rekening mee te houden zodat de er geen dubbeltellingen ontstaan in inkomen en waarde.

Conclusie
Bij het waarderen van een onderneming bij echtscheiding krijgt een waardeerder te maken met emoties en spraakverwarring over waarderingstechnieken en uitgangspunten. Deze worden vaak gedreven door doelargumentatie van partijen.
Het toepassen van de juiste methodiek is van essentieel belang. De DCF methodiek is altijd juist, de rentabiliteitswaarde kan een juiste uitkomst geven, mits goed toegepast en wanneer voldaan wordt aan een aantal uitgangspunten.
De uitgangspunten worden per definitie gedreven door subjectieve aannames. Wanneer partijen lijnrecht tegenover elkaar staan dient de waardeerder op basis van relevante gegevens en hoor en wederhoor zijn eigen aannames te doen en te verantwoorden.
Bij de waardering van de onderneming is het ondernemersinkomen een variabele die de hoogte van de waardering beïnvloedt. Dit inkomen is ook de grondslag voor de draagkrachtberekening voor alimentatie. Vaak worden deze aspecten in afzonderlijke procedures behandeld. De waardeerder dient alert te zijn op inconsistenties en dubbeltellingen.

Neem contact op voor een vrijblijvend gesprek

    Disclosure Statements

    DOWNLOAD

    In onze ‘disclosure statements’ vindt u een overzicht van onze ervaringsachtergrond. U kunt ze hier downloaden.